| Keywords and phrases: 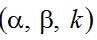 -resolvent family, -resolvent family, 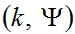 -Hilfer Sobolev type fractional differential equations, Mild solution, existence. -Hilfer Sobolev type fractional differential equations, Mild solution, existence.
Received: June 2, 2024; Accepted: July 26, 2024; Published: August 9, 2024
How to cite this article: Haihua Wang, Jie Zhao, Junhua Ku and Yanqiong Liu, Existence of mild solution for 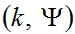 -Hilfer fractional Cauchy value problem of Sobolev type, Advances in Differential Equations and Control Processes 31(4) (2024), 439-472. https://doi.org/10.17654/0974324324024 -Hilfer fractional Cauchy value problem of Sobolev type, Advances in Differential Equations and Control Processes 31(4) (2024), 439-472. https://doi.org/10.17654/0974324324024
This Open Access Article is Licensed under Creative Commons Attribution 4.0 International License  
References:
[1] Y. K. Chang, A. Pereira and R. Ponce, Approximate controllability for fractional differential equations of Sobolev type via properties on resolvent operators, Fract. Calc. Appl. Anal. 20 (2017), 963-987.
[2] K. Diethelm and A. D. Freed, On the solution of nonlinear fractional order differential equations used in the modeling of viscoelasticity, Scientific Computing in Chemical Engineering II, Springer-Verlag, Heidelberg (1999), 217-224.
[3] L. Gaul, P. Klein and S. Kempfle, Damping description involving fractional operators, Mech. Systems Signal Process. 5 (1991), 81-88.
[4] W. G. Glockle and T. F. Nonnenmacher, A fractional calculus approach of self- similar protein dynamics, Biophys. J. 68 (1995), 46-53.
[5] I. Haque, J. Ali and M. Mursaleen, Existence of solutions for an infinite system of Hilfer fractional boundary value problems in tempered sequence spaces, Alx. Eng. J. 65 (2023), 575-583.
[6] R. Hilfer, Applications of Fractional Calculus in Physics, World Scientific, Singapore, 2000.
[7] R. Hilfer, Applications of Fractional Calculus in Physics, World Scientific, 2000.
[8] F. Jarad and T. Abdeljawad, Generalized fractional derivatives and Laplace transform, Discrete. Contin. Dyn. Syst. 13 (2012), 709-722.
[9] A. A. Kilbas, H. M. Srivastava and J. J. Trujillo, Theory and Applications of Fractional Differential Equations, North-Holland Mathematics Studies, 204, Elsevier, Amsterdam, 2006.
[10] K. D. Kucche and A. D. Mali, On the nonlinear -Hilfer fractional differential equations, Chaos Soliton Fract. 152 (2021), 111335.
[11] Y. C. Kwun, G. Farid, W. Nazeer, S. Ullah and S. M. Kang, Generalized Riemann-Liouville k-fractional integrals associated with Ostrowski type inequalities and error bounds of Hadamard inequalities, IEEE Access 6 (2018), 64946-64953.
[12] L. S. Liu, F. Guo, C. X. Wu and Y. H. Wu, Existence theorems of global solutions for nonlinear Volterra type integral equations in Banach spaces, J. Math. Anal. Appl. 309 (2005), 638-649.
[13] B. Maayah, A. Moussaoui, S. Bushnaq and O. Abu Arqub, The multistep Laplace optimized decomposition method for solving fractional-order coronavirus disease model (COVID-19) via the Caputo fractional approach, Demonstratio Mathematica 55 (2022), 963-977.
[14] R. Ponce, Existence of mild solutions to nonlocal fractional Cauchy problems via compactness, Abatr. Appl. Anal. (2016), 4567092.
[15] J. Sabatier, O. P. Agrawal and J. A. T. Machado, Advances in Fractional Calculus: Theoretical Developments and Applications in Physics and Engineering, Springer, Dordrecht, The Netherlands, 2007.
[16] S. G. Samko, A. A. Kilbas and O. I. Marichev, Fractional Integrals and Derivatives, Theory and Applications, Gordon and Breach Science Publishers, Yverdon, 1993.
[17] J. Sausa and E. De Oliveira, On the -Hilfer fractional derivative, Commun. Nonlinear Sci. Numer. Simul. 60 (2018), 72-91.
[18] L. W. Weis, A generalization of the Vidav-Jorgens perturbation theorem for semigroups and its application to transport theory, J. Math. Anal. Appl. 129 (1988), 6-23.
|