JP Journal of Geometry and Topology
Volume 30, Issue 2, Pages 143 - 154
(December 2024)
http://dx.doi.org/10.17654/0972415X24010 |
|
FOLDING MOTION IN 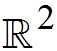 THAT SHRINKS A GOOD POLYGONAL ANNULUS TO ARBITRARY SMALL NEIGHBORHOOD OF THE INNER BOUNDARY THAT SHRINKS A GOOD POLYGONAL ANNULUS TO ARBITRARY SMALL NEIGHBORHOOD OF THE INNER BOUNDARY
Hiroko Murai
|
Abstract:
In 2004, Demaine et al. showed that if P is a simply connected polygonal region in the plane, then for any piecewise- folded state of P, there exists a folding motion from P to [1]. We have shown that if P is not simply connected, then the conclusion of the theorem does not necessarily hold, in fact, there exists an annulus P in such that there exists a piecewise- folded state of P which does not admit folding motions from P by using “knot and link theory”. From the viewpoint of knot and link theory, it is reasonable to expect that the folded state admits a folding motion from P if and only if forms a trivial link in (Conjecture). Note that the ‘only if’ part of the Conjecture is obvious. In this paper, we give a proof of the following statement that will be used in an expected proof of the ‘if’ part of the Conjecture for special kind of annulus P.
If is an annulus such that each of the boundary components bounds a polygonal convex region, then for any there exists a flat folded state such that is contained in the -neighborhood of the inner boundary of P in P, denoted by with a strongly flat folding motion from P to which satisfies the following:
(1) For any the number of 1-simplices of the 1-complex is finite, where denotes the canonical crease pattern
(2) For any is a good polygonal annulus.
(3) For any with we have |
| Keywords and phrases: origami, folding motion, flat folded state, polygonal annulus.
Received: October 17, 2024; Accepted: November 25, 2024; Published: December 24, 2024
How to cite this article: Hiroko Murai, Folding motion in that shrinks a good polygonal annulus to arbitrary small neighborhood of the inner boundary, JP Journal of Geometry and Topology 30(2) (2024), 143-154. https://doi.org/10.17654/0972415X24010
This Open Access Article is Licensed under Creative Commons Attribution 4.0 International License  
References:
[1] Erik D. Demaine, Satyan L. Devadoss, Joseph S. B. Mitchell and Joseph O’Rourke, Continuous foldability of polygonal paper, Proc. of CCCG’04, Montréal, 2004, pp. 64-67.
[2] Erik D. Demaine and Joseph O’Rourke, Geometric Folding Algorithms: Linkages, Origami, Polyhedra, Cambridge University Press, New York, 2007.
[3] Akari Iwamura and Hiroko Murai, Existence of folded states which do not admit folding motions from the unfolded state, JSIAM Letters 16 (2024), 101-104.
|
| |
| Number of Downloads: 9 | Number of Views: 16 |
|